Networkbridge NBO

Prime Number Universe: The Riemann Hypothesis (1859)

New pattern detection through alternative number bases and systematic visualization

Contents

1. Introduction: Making prime numbers visible
2. Observed regularities / patterns
3. The three software tools used
4. Software 1 – Decimal system (base 10)
5. Software 2 – Freely selectable base
6. Software 3 – Large bases (beyond base 36)
7. Your own experiments – step by step
8. Purpose / aim
9. Examples: prime number tables generated by Software 1-3
10. RGUMS Prime Numbers Software 1-3: highlight / copy

1. Introduction: Making prime numbers visible

Prime numbers have been considered mysterious for centuries. They are clearly defined, yet difficult to predict. Despite intensive research, our basic understanding of their internal structure has changed only slightly since the Riemann Hypothesis was published in 1859.
This page takes a different approach. Instead of proposing new theories, it makes prime numbers visible—using tables designed so that patterns are not primarily calculated, but seen.

2. Observed regularities / patterns

When large ranges of prime numbers are displayed in tables using the software tools listed below, recurring structures become visible:
In the decimal system (base 10), what I call “pairs” appear—two primes occurring as immediate neighbors in the table. In the ranges shown here, these groups do not grow beyond two consecutive primes.
In a number system with 42 digits (base 42), corresponding groups of four appear, again not larger.
In bases such as 9 or 11, these “pairs” do not appear at all.
End digits such as 2, 4, 5, 6, 8, and 0, which do not occur for primes in base 10 (except among the very smallest primes), behave differently in other number bases.

3. The three software tools used

To reproduce and extend these observations, three simple software variants are provided. All three use the same definition of prime numbers, but they differ in how numbers are represented and arranged. They are designed so that no mathematical background is required.

4. RGUMS Prime Numbers – Software 1: Decimal system (base 10)

You only need to enter the range for the prime number table. A double click on the generated file opens it immediately in your browser.
Change these values in the code:

<title>Prime Number Table (1–1000)</title> → change the displayed range
let zahl = 1; → change the starting value
for (let zeile = 0; zeile < 100; zeile++) { → change the number of rows

5. RGUMS Prime Numbers – Software 2: Freely selectable base

The decimal system is not a necessity—it is a convention. We use ten digits because we have ten fingers. With eight or twelve fingers, we might have adopted different number systems.
In this software, you can choose the base yourself, for example base 16:

const BASE = 16; → change 16 to any base you want (within the limits of the software)

The logic of prime numbers remains valid—but the visible patterns can change significantly, as shown in the attached PDF examples.

6. RGUMS Prime Numbers – Software 3: Large bases (beyond base 36)

This version is designed to display very large bases. Three values are especially important and should be chosen consistently—for example base 42:

const BASE = 42; // change 42
const START = 1; // change 1
const ROWS = 100; // 100 × 42 = 4200 numbers (change 100)
const COLS = 42; // change 42 (should match BASE)
const DIGITS = "0123456789ABCDEFGHIJKLMNOPQRSTUVWXYZabcdef";

BASE defines the number base
COLS defines the number of columns in the table
DIGITS defines which characters are used as digits
If you want a base larger than 42, you can simply append additional lowercase letters to the DIGITS string.

7. Your own experiments – step by step

Open a text editor
Paste the copied RGUMS Prime Numbers HTML code
Change the numbers / values as needed
Choose File → Save As
Select the location (e.g., Desktop)
Enter a filename and end it with .html
Make sure “All files” is selected
Save
Double-click the saved file to open it in your browser

8. Purpose / aim

The provided tables and PDF documents serve as visual reference material. They are intended to encourage comparison of known properties of prime numbers across different number bases and table layouts—and to help identify additional patterns.
The approach is deliberately open and exploratory. It is aimed both at readers with mathematical training and at interested observers without formal education, because the key structures are made directly accessible through visualization.

9a. Examples: prime number tables generated by Software 1

Base 10, decimal system

9b. Examples: prime number tables generated by Software 2

Base 16, Freely chosen system

9c. Examples: prime number tables generated by Software 3

Base 42, Freely chosen system

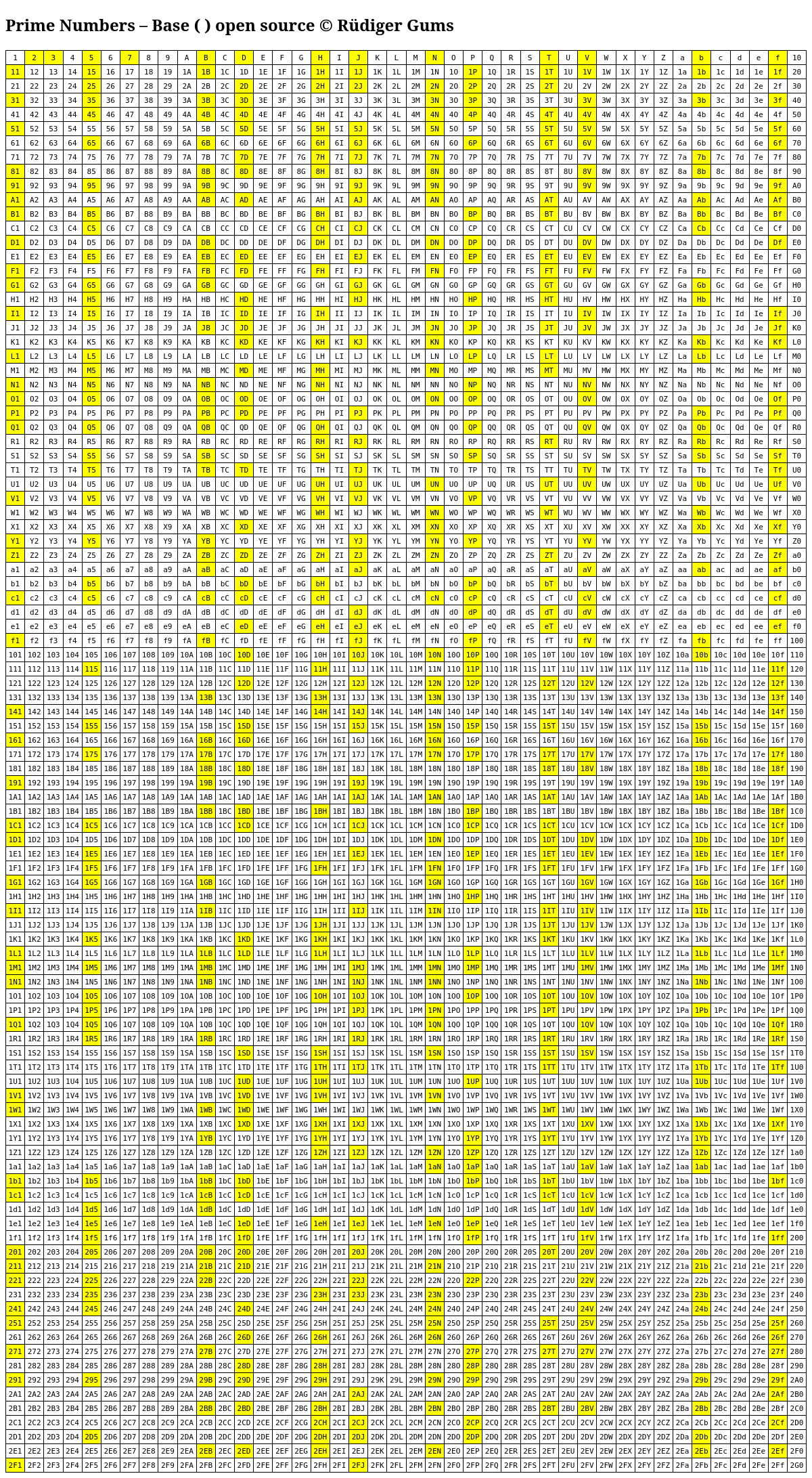
10a. RGUMS Prime Numbers Software 1: highlight / copy

<!DOCTYPE html>

<html>

<head>

<title>Primzahlen-Tabelle (1–1000)</title>

<style>

table { border-collapse: collapse; width: 100%; }

th, td { border: 1px solid black; padding: 4px; text-align: center; }

.prime { background-color: yellow; }

</style>

</head>

<body>

<h2 id="headline"></h2>
<h2>Prime Numbers – Base ( ) open source © Rüdiger Gums
</h2>

</table>

// Funktion, um zu prüfen, ob eine Zahl eine Primzahl ist

function istPrimzahl(num) {

if (num <= 1) return false;

if (num === 2) return true;

if (num % 2 === 0) return false;

for (let i = 3; i <= Math.sqrt(num); i += 2) {

if (num % i === 0) return false;

}

return true;

}

// Tabelle mit 1000 Zeilen und 10 Spalten füllen

function fuelleTabelle() {

const table = document.getElementById("primzahlTabelle");

let zahl = 1;

for (let zeile = 0; zeile < 100; zeile++) {

const row = document.createElement("tr");

for (let spalte = 0; spalte < 10; spalte++) {

const cell = document.createElement("td");

cell.textContent = zahl;

// Primzahlen gelb markieren

if (istPrimzahl(zahl)) {

cell.classList.add("prime");

}

row.appendChild(cell);

zahl++;

}

table.appendChild(row);

}

// Tabelle beim Laden der Seite füllen

window.onload = fuelleTabelle;

</script>

</body>

</html>

10b. RGUMS Prime Numbers Software 2: highlight / copy

<!DOCTYPE html>
<html lang="de">
<head>
<meta charset="UTF-8" />
<title>Primzahlen-Tabelle (Basis 16)</title>
<style>
table { border-collapse: collapse; width: 100%; font-family: monospace; }
td { border: 1px solid black; padding: 4px; text-align: center; }
.prime { background-color: yellow; }
</style>
</head>
<body>
<h2 id="headline"></h2>
<h2>Prime Numbers – Base ( ) open source © Rüdiger Gums
</h2>
<table id="primzahlTabelle"></table>
<script>
// ======= Einstellungen =======
const BASE = 16; // <-- 15 für Basis-15 (0-9,A-E) oder 16 für Hex (0-9,A-F)
const START = 1; // <-- 1 wie bisher; wenn du wirklich bei 0 starten willst: 0
const ROWS = 1000; // Anzahl Zeilen
// Spalten passend zur Basis (Basis-15 => 15 Spalten, Basis-16 => 16 Spalten)
const COLS = BASE;
// ============================
// Primzahltest (intern "normal" gerechnet – unabhängig von der Basis-Darstellung)
function istPrimzahl(num) {
if (num <= 1) return false;
if (num === 2) return true;
if (num % 2 === 0) return false;
for (let i = 3; i <= Math.sqrt(num); i += 2) {
if (num % i === 0) return false;
}
return true;
}
// Dezimalzahl -> Darstellung in Basis BASE (Buchstaben groß)
function toBaseN(num) {
return num.toString(BASE).toUpperCase();
}
function fuelleTabelle() {
document.getElementById("headline").textContent =
`Prime Numbers Base ${BASE} (Start: ${START})`;
const table = document.getElementById("primzahlTabelle");
let zahl = START;
for (let r = 0; r < ROWS; r++) {
const row = document.createElement("tr");
for (let c = 0; c < COLS; c++) {
const cell = document.createElement("td");
// Anzeige im gewünschten Zahlensystem
cell.textContent = toBaseN(zahl);
// Markierung echter Primzahlen (zahl ist die "Zahl an sich", nicht die Schreibweise)
if (istPrimzahl(zahl)) {
cell.classList.add("prime");
}
row.appendChild(cell);
zahl++;
}
table.appendChild(row);
}
}
window.onload = fuelleTabelle;
</script>
</body>
</html>

10c. RGUMS Prime Numbers Software 3: highlight / copy

<!DOCTYPE html>

<head>

<title>Primzahlen-Tabelle – Basis 42</title>

<style>

table {

border-collapse: collapse;

width: 100%;

font-family: monospace;

font-size: 11px;

}

td {

border: 1px solid black;

padding: 3px;

text-align: center;

}

.prime {

background-color: yellow;

}

</style>

</head>

<body>

<h2>Prime Numbers – Base ( ) open source © Rüdiger Gums

</h2>

// =====================

const BASE = 42;

const START = 1;

const ROWS = 100; // 100 × 42 = 4200 Zahlen

const COLS = 42;

const DIGITS = "0123456789ABCDEFGHIJKLMNOPQRSTUVWXYZabcdef";

// =====================

function istPrimzahl(n) {

if (n <= 1) return false;

if (n === 2) return true;

if (n % 2 === 0) return false;

for (let i = 3; i <= Math.sqrt(n); i += 2) {

if (n % i === 0) return false;

}

return true;

}

function toBase42(n) {

if (n === 0) return "0";

let out = "";

let num = n;

while (num > 0) {

const r = num % BASE;

out = DIGITS[r] + out;

num = Math.floor(num / BASE);

}

return out;

}